이 글은 edwith - [부스트코스] 텐서플로우로 시작하는 딥러닝 기초의 개인적인 공부기록이므로 오류가 있을 수 있습니다!
3번 글의 가설에서 b(y절편)을 빼고 간단하게 만든 후 Python으로 직접 Cost Function과 Gradient Descent를 구현해보자.
-
기존 가설


-
간단 가설


다음과 같이 진행된다.
Cost Function
# Cost Function in pure Python
X = np.array([1, 2, 3])
Y = np.array([1, 2, 3])
def cost_func(W, X, Y):
c = 0
for i in range(len(X)):
c += (W * X[i] - Y[i]) ** 2 # cost function과 동일
return c / len(X)
print(" W | cost")
for feed_W in np.linspace(-3, 5, num=15):
curr_cost = cost_func(feed_W, X, Y)
print("{:6.3f} | {:10.5f}".format(feed_W, curr_cost))X는 [1, 2, 3], Y도 [1, 2, 3]이다.
cost_func 함수는 W, X, Y 3개의 인자를 받고 cost(w)의 시그마를 for loop를 이용해 시행한 후 return에서 X의 개수만큼 나눠 평균을 return 하고 있다.
feed_W의 for loop에서는 -3과 5 사이를 15개의 구간으로 나눠서(linspace) 돌고 있다.
W가 -3일때부터 cost를 구하기 시작, 5까지 연산을 돈 뒤 멈출 것이다.
curr_cost는 cost_func의 결과이며 w값에 따라 cost가 어떻게 변화하는지 보여줄 것이다.
우리가 기대하는 W의 값은 1이고 당연히 이때 cost는 0을 기대한다.
W | cost
-3.000 | 74.66667
-2.429 | 54.85714
-1.857 | 38.09524
-1.286 | 24.38095
-0.714 | 13.71429
-0.143 | 6.09524
0.429 | 1.52381
1.000 | 0.00000
1.571 | 1.52381
2.143 | 6.09524
2.714 | 13.71429
3.286 | 24.38095
3.857 | 38.09524
4.429 | 54.85714
5.000 | 74.66667
위 Python 코드의 연산은 다음과 같은 결과를 보여준다.
기대했던 대로 W가 1일때 cost는 0이 되는 것을 볼 수 있다.
Gradient Descent
Gradient Descent는 cost의 최솟값(1차 근삿값)을 찾아주는 방법 중 하나다.
- 랜덤한 x값 / y값에서 출발한다. (0, 0)일 수도 (1, 1)일 수도 있다.
- 함수의 기울기가 낮은 쪽으로 W값과 b값을 조금씩 이동시킨다.
- 극값에 이를때까지 반복.
함수의 극값은 미분값을 이용해 구할 수 있다.
사실 tensorflow에서 Gradient Descent를 위한 함수를 이미 제공하고 있지만(3번 글의 GradientTape, Gradient 함수) 직접 구현하면 다음과 같다.
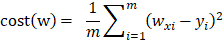



미분의 과정을 통해 w값을 최종과 같은 형태로 갱신해나갈 수 있다.
알파는 learning rate이며 초기에 임의의 값으로 설정할 수 있다.
learning rate는 보통 0.1 ~ 0.001 사이에서 시작하는데, 너무 작으면 반영이 많이 되지 않아 효율성이 떨어지고 너무 커지면 변하는 범위가 너무 커져서 극값에 도달하지 못할 수 있기 때문에 적당한 범위를 설정하도록 한다. 연산의 결과에 따라 learning rate를 가변적으로 설정하기도 한다.
Python으로 Gradient Descent를 구현해보면 다음과 같다.
tf.random.set_seed(0)
x_data = [1., 2., 3., 4.]
y_data = [1., 2., 3., 4.]
W = tf.Variable(tf.random.normal([1], -100., 100.)) # (차원, start, end)
for step in range(300):
hypothesis = W * x_data
cost = tf.reduce_mean(tf.square(hypothesis - y_data))
alpha = 0.02 # learning rate
gradient = tf.reduce_mean(tf.multiply(tf.multiply(W, x_data) - y_data, x_data))
descent = W - tf.multiply(alpha, gradient)
W.assign(descent)x_data와 y_data는 같기 때문에 위와 같이 W값은 1을 기대한다.
W는 -100과 100 사이의 숫자 하나를 랜덤으로 설정한다.
300번의 학습을 시행하며 hypothesis와 cost는 위의 간단 가설과 동일하나 cost의 시그마를 reduce_mean 함수로 시행했다는 점이 다르다.
learning rate는 0.02로 초기값을 설정한다. 먼저 기울기를 구한다. 미분 과정 최종 중 1/m부터 끝까지의 수식을 코드로 구현했다.
descent는 설정한 learning rate를 반영한 gradient값이며 assign 메서드를 이용해 W에 이를 반영시킨다.
연산 10번 단위로 cost와 W를 출력해보면 다음과 같다.
step | cost | W
0 | 18829.7812 | 43.590324
10 | 729.8335 | 9.384944
20 | 28.2880 | 2.650781
30 | 1.0964 | 1.324997
40 | 0.0425 | 1.063983
50 | 0.0016 | 1.012597
60 | 0.0001 | 1.002480
70 | 0.0000 | 1.000488
80 | 0.0000 | 1.000096
90 | 0.0000 | 1.000019
100 | 0.0000 | 1.000004
110 | 0.0000 | 1.000001
120 | 0.0000 | 1.000000
130 | 0.0000 | 1.000000
140 | 0.0000 | 1.000000
150 | 0.0000 | 1.000000
160 | 0.0000 | 1.000000
170 | 0.0000 | 1.000000
180 | 0.0000 | 1.000000
190 | 0.0000 | 1.000000
200 | 0.0000 | 1.000000
210 | 0.0000 | 1.000000
220 | 0.0000 | 1.000000
230 | 0.0000 | 1.000000
240 | 0.0000 | 1.000000
250 | 0.0000 | 1.000000
260 | 0.0000 | 1.000000
270 | 0.0000 | 1.000000
280 | 0.0000 | 1.000000
290 | 0.0000 | 1.000000
cost는 0에, W는 1에 수렴하는 것을 볼 수 있다.
'인공지능 > ML' 카테고리의 다른 글
| 인공지능 6. Logistic Regression (0) | 2020.03.30 |
|---|---|
| 인공지능 5. Multi Variable Linear Regression (0) | 2020.03.27 |
| 인공지능 3. Simple Linear Regression 구현 (0) | 2020.03.24 |
| 인공지능 2. Simple Linear Regression (0) | 2020.03.23 |



